Братишка, ты цел?
09:21 17/05/2013 Наука и техника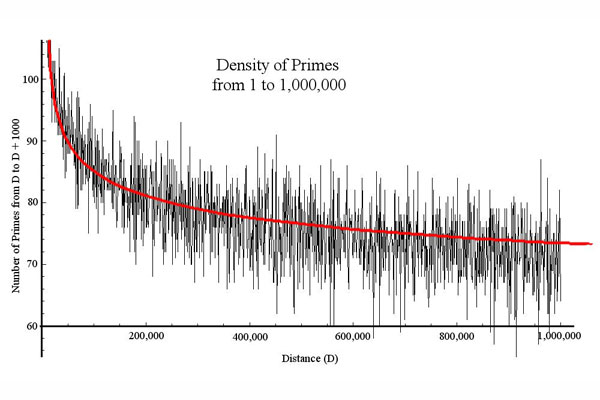
Американский математик Итан Чжан представил работу, которая может считаться важнейшим шагом на пути решения задачи о простых числах-близнецах — по некоторым данным, одной из старейших нерешенных проблем в математике. Работа принята вAnnals of Mathematicsи, судя по первым отзывам рецензентов, ошибок не содержит. В открытом доступе статьи пока нет, но записи с семинара, который Чжан провел в Гарвардском университете, уже гуляют по Сети.
Простыми называются числа, которые делятся только на единицу и на себя (для удобства 1 в множество простых не включается). Они всегда интересовали математиков, ведь именно простые числа составляют кирпичики, из которых построены все остальные числа — хорошо известно, что всякое число единственным образом разлагается в произведение простых чисел (необязательно попарно различных).
Самые естественные вопросы, возникающие в связи с этим у математиков, касаются строения множества простых чисел. Несмотря на то, что большинство таких вопросов, как правило, формулируется очень просто, ответы на них не просто сложны. Чаще всего они оказываются результатом целых теорий, которые, как водится, имеют кучу полезных приложений — от криптографии до квантовой механики, но создавались исключительно для того, чтобы ответить на эти самые вопросы.
Прежде всего возникает вопрос о том, конечно ли множество простых чисел. Ответ хорошо известен со школы: множество простых чисел бесконечно, и это легко доказать. Действительно, пусть это не так и множество простых чисел конечно. Обозначим эти числа через p1, p2, ... pn и рассмотрим число p1p2....pn + 1. Легко увидеть, что это число не делится ни на одно из перечисленных простых чисел, и, стало быть, среди его простых делителей есть числа, которые в наш список не попали. Это противоречие и завершает наше доказательство. Точнее, не наше, а Евклида, опубликованное в 9-м томе его «Начал».
Если простых чисел бесконечное множество, то возникает другой вопрос: как они расположены в ряду натуральных чисел? Нет ли для них, например, формулы? Выписывание первых нескольких чисел (скажем, 2, 3, 5, 7, 11, 13, 17, 19) совершенно не проясняет (по крайней мере автору) ситуацию. На настоящий момент известно несколько результатов, касающихся строения этого множества. Этим вопросом (о формуле) занимался Эйлер. Ему, например, принадлежит следующее наблюдение: квадратичный трехчлен n2 − n + 41 дает простые значения для всех натуральных n, не превосходящих 40. Быть может, тогда существует подходящая формула в виде многочлена? Легко доказывается, что такой формулы, конечно, нет. Впрочем, некоторое подобие формулы получить можно (см. врез выше).
Если эффективной формулы для множества простых чисел нет, то, решили математики, его следует изучать другими методами. Например, насколько редко могут быть расположены простые числа? Оказывается, последовательные отрезки числового ряда, не содержащие ни одного простого числа, могут быть сколь угодно длинными. Действительно, возьмем произвольное натуральное число n и рассмотрим отрезок натурального ряда вида (n + 1)! + 2, (n + 1)! + 3, ..., (n + 1)! + n + 1. Каждое из представленных чисел составное: первое делится на 2, второе — на 3, третье — на 4 и так далее. Стало быть, простые числа могут быть сколь угодно «разреженными». Более того, можно сказать, что в некотором смысле расстояние между соседними простыми числами в среднем растет как log p.
Соответственно, возникает следующий вопрос: а какое минимальное расстояние может быть между двумя простыми числами? Пусть это расстояние 1, то есть числа p и p + 1 простые одновременно. Учитывая, что четные и нечетные числа в числовом ряду чередуются, получаем, что одно из этих чисел должно быть четным, то есть делиться на 2. Если учесть, что по нашему (сугубо техническому) соглашению 1 не является простым числом, то существует одна-единственная такая пара простых чисел — это 2 и 3. Следовательно, расстояние между любыми двумя соседними другими простыми числами — как минимум два. Простые числа, расстояние между которыми равно двум, и называются числами-близнецами.
Первые несколько пар чисел-близнецов легко перечислить — это (3, 5), (5, 7), (11, 13), (17, 19) и так далее. Самая большая пара чисел-близнецов из известных на настоящий момент была открыта в декабре 2011 года в рамках проекта распределенных вычислений PrimeGrid. Она имеет вид (3756801695685 · 2666669 — 1, 3756801695685 · 2666669 + 1). В десятичной записи каждого из этих чисел по 200700 знаков. Это, конечно, очень большие числа, и само их существование ставит такой вот вопрос: конечно ли множество чисел-близнецов? Этот вопрос, точнее предположение о бесконечности этого множества, и носит название «гипотезы о числах-близнецах». Тут важно понимать, что бесконечность множества чисел-близнецов ни в коем случае не противоречит утверждению о логарифмическом росте расстояний между простыми числами — рост просто означает, что исключений (не укладывающихся в общую тенденцию чисел) достаточно мало.
Довольно часто гипотезу о числах-близнецах приписывают Евклиду. Разумеется, такого рода утверждения были грекам по силам, однако убедительных подтверждений этого факта нет. Впервые в печатной литературе эта гипотеза была высказана в 1849 году Альфонсом де Полиньяком в более общем виде: для любого четного числа 2k множество таких соседних простых чисел (то есть между которыми нет других простых), чтобы расстояние между ними в точности равнялось 2k, бесконечно. При k = 1 получаем оригинальную формулировку. Что касается термина «числа-близнецы», то он был введен в обиход математиком Вигго Бруном. Брун изучал разного рода простые числа и в 1915 году доказал замечательную теорему, о которой, пожалуй, следует рассказать чуть более подробно.
Гармоническим рядом называется последовательность дробей 1/n. Известно, что, несмотря на убывание величин этой последовательности, сумма этого ряда бесконечно большая: то есть, для любого наперед заданного числа можно подобрать такое N, что сумма первых N членов гармонического ряда будет больше этого числа. При этом, если брать не все натуральные n, а только простые, то есть рассмотреть последовательность 1/pn, где pn — последовательно занумерованные простые числа, то сумма полученного ряда все равно будет бесконечно большой (еще математики говорят, что такой рядрасходится).
Брун решил рассмотреть последовательность, состоящую только из чисел-близнецов. Если бы такой ряд расходился, то из этого немедленно бы вытекало утверждение гипотезы о числах-близнецах — ясное дело, сумма конечного числа чисел не бесконечна. Однако, оказалось, что сумма полученного ряда не только конечна (математики в таком случае говорят, что рядсходится), но и равна достаточно небольшому числу, известному как константа Бруна B2. Она примерно равна 1,902160583104. То есть теорема Бруна является еще одним подтверждением того, что пар чисел-близнецов по сравнению с остальными простыми числами немного.
Интерес Бруна к числам-близнецам был инспирирован, среди прочего, выступлением Эдмунда Ландау на Пятом Международном конгрессе математиков в 1912 году. Тогда Ландау сформулировал четыре задачи из теории чисел, решение которых, по его мнению, было недостижимо для математиков того времени. Гипотеза о числах-близнецах была одной из этих проблем. На самом деле за прошедшие 100 лет ситуация несколько изменилась, но только не для гипотезы о числах-близнецах (например, тринарная проблема Гольдбаха для достаточно больших чисел была решена в 1937 году Виноградовым). При этом большинство математиков уверены в истинности гипотезы о числах-близнецах. Например, самое свежее неправильное доказательство этого утверждения датируется 2004 годом.
Да что там гипотеза! До последнего времени не был понятен даже такой факт. Рассмотрим множество Mk из гипотезы Полиньяка соседних простых чисел, расстояние между которыми равно 2k. Бесконечно ли это множество хоть для какого-нибудь k? Лишь только теперь математик из США Итан Чжан показал, что для некоторого k, не превосходящего 35 миллионов, такое множество действительно бесконечно. На первый взгляд может показаться, что 35 миллионов от 1 (речь про k) очень уж далеки, но не для математики.
Итак, что же сделал Чжан? Он взял более раннюю работу своего коллеги и немного подправил функции, которые там фигурировали (более подробно доказательство изложено здесь). При этом, что особенно удивительно и что даже вызвало подозрения на первом этапе анализа доказательства, Чжан использовал уже существующую технику. В этом смысле его доказательство разительно отличается от, например, недавнего доказательства ABC-гипотезы Синити Мотидзуки (тоже, кстати, ключевой проблемы теории чисел, которую часто упоминают в одном ряду с гипотезой о числах-близнецах). Доказательство Мотидзуки занимает свыше 500 страниц и содержит целую теорию — с момента публикации прошло полгода, а результаты его проверки до сих пор неизвестны. Скорее всего, математики, занимающиеся этой самой проверкой, до сих пор не добрались до конца работы.
Статья Чжана, напротив, довольно проста. Более того, ее рецензенты изAnnals of Mathematics— журнала, куда она была подана — заявили, что судя по всему работа верна. Главное, впрочем, даже не это — не исключено, что метод Чжана еще можно будет подправить, так что, возможно, значение k удастся уменьшить. Сам математик почти уверен, что до 1 дело не дойдет, но что можно «сбить» с 35 миллионов, он не сомневается.
Вместо заключения
Здесь, по хорошей традиции, автор должен попытаться ответить на вопрос пытливого читателя: «А зачем все это нужно?» В этот раз ответ будет в виде байки.
В 1994 году математик Томас Найсли вычислял константу Бруна. Делал он это грубой силой, то есть считая сумму дробей для пар чисел-близнецов. Когда дело дошло до пары (824 633 702 441, 824 633 702 443), в машинной выдаче обнаружились странности. В частности, суммы, посчитанные до добавления в сеть новых мощных машин на базе Pentium, отличались от цифр, полученных после. Проведя несколько испытаний, Найсли пришел к выводу, что в процессорах Intel имеется какой-то дефект в системе деления чисел с плавающей точкой. Несмотря на то, что неправильный результат в среднем выдавался в одном случае из 9 миллиардов, новость о наличии бага привела к тому, что в 1995 году корпорация Intel потратила 475 миллионов долларов на замену содержащих дефект процессоров. Такие дела.
Андрей Коняев
Комментирование разрешено только первые 24 часа.
Комментарии(81):
| 0 +0−0 | Св. Валентин | 13:43:25 18/05/2013 | ||||||
| ||||||||
т.е. доказали что всегда найдутся два простых числа, таких что |Х1-Х2|<=35000000 | ||||||||
| 0 +0−0 | Nikolay Lozhkarev | 02:30:03 18/05/2013 |
Я думал, что это не многочлен Джонса, а многочлен Матиясевича? | ||
| 0 +1−1 | Vladimir Lenok | 01:54:53 18/05/2013 |
Неплохо, только вот язык немного простанародный. Это всё таки математика, а не статья о съезде колхозников. | ||
| 0 +0−0 | Baron Samedi | 00:55:16 18/05/2013 | ||||||
| ||||||||
Ок. Может мне и в самом деле кажется. | ||||||||
| 0 +0−0 | Mr. Smith Herr Hase | 19:45:51 17/05/2013 | ||||||
| ||||||||
Вы же не bydlo | ||||||||
| 0 +0−0 | Alex Alex | 19:10:56 17/05/2013 |
Андрей, математика - прикладная наука? | ||
| 0 +1−1 | Vasily Voronin | 18:21:36 17/05/2013 | ||||||
| ||||||||
Это лучше, чем сказать: сумма ряда бесконечно большая (что это такое я вам не скажу, вы просто мне поверьте). В рамках средней школы вообще много всего интересного проходят, только многие это благополучно забывают. Например, помните, что такое репликация ДНК или митоз? Насчёт статей - все хорошие учёные пишут статьи по-английски, а иначе про твоё открытие никто не узнает. При этом если не учить английский в школе, то потом выучить на порядок сложнее | ||||||||
| 0 +0−0 | Artyom Petrenkov | 17:25:26 17/05/2013 | ||||||
| ||||||||
Можете почитать книгу "Простая одержимость" Джона Дербишира. Но сразу предупреждаю: есть большая вероятность стать "ферматистом"-риманистом. | ||||||||
| 0 +1−1 | Vasily Voronin | 16:09:50 17/05/2013 | ||||||
| ||||||||
Вот-вот, Теренцу Тао в прошлом году стукнуло 37, и он видимо почувствовал приближение маразма | ||||||||
| 0 +2−2 | Andrei Konyaev | 11:49:49 17/05/2013 | ||||||
| ||||||||
Крутая ссылка. Ваще болт положили на результат Виноградова, как будто его и не было. Отлично просто | ||||||||
| 0 +3−3 | Vasily Voronin | 10:48:24 17/05/2013 | ||||||
| ||||||||
Кстати, можно в статье сделать примечание, что n! означает факториал. В некоторых школах этого не проходят | ||||||||
| 0 +3−3 | Николай Камю | 09:48:32 17/05/2013 |
А жизнь весёлый карнавал. | ||
| -1 +0−1 | Baron Samedi | 15:47:28 17/05/2013 | ||||||
| ||||||||
Мне кажется, что они тут не очень нужны. И что если бы Андрей просто сказал, что всегда можно найти пятьдесят, сто, миллион составных чисел подряд - ему бы и так все поверили. А формула, доказывающая их существование, только заставит половину читателей дропнуть на ней. | ||||||||
| -2 +1−3 | A Z | 14:32:56 19/05/2013 |
Думаю, многие числовые теории будут решены, когда люди перейдут с десятичной системы на какую-то правильную. | ||
| -2 +5−7 | макс ривкин | 13:21:27 18/05/2013 | ||||||
| ||||||||
Врядли такие статьи читают люди со школьным курсом. Им это просто не интересно. | ||||||||
| -2 +2−4 | Baron Samedi | 13:57:48 17/05/2013 |
Скажите, неужели и вправду здесь есть хоть один не-математик, который не дропнул статью, глядя на все эти формулы? Я бы дропнул, например. | ||
| -4 +0−4 | Baron Samedi | 16:16:00 17/05/2013 | ||||||
| ||||||||
Ох да. Без формул читатели не ощутят духовности. | ||||||||
| -4 +5−9 | Наум Приходящий | 14:59:22 17/05/2013 |
опять наверное амырыканцы что то затевают против РФ и её вождя ВладымыраВлыдымыровича! - ведь не спроста они это всё придумали.... вчера вот хоккей а сёдня эти как их... числа-братья ёп та. Не спроста это всё. Давайте разбираться вместе на сайте Николая Старикова! | ||
| -7 +3−10 | Baron Samedi | 14:15:16 17/05/2013 |
Даже внезапно понял, какое чувство вызывает у меня весь этот сугубо математический лексикон в популяризирующей статье. Все равно что translate на русский тексты с english, и при этом оставлять some words непереведёнными, надеясь in such a manner привить bydlo любовь к английскому language. | ||
| -12 +1−13 | Anon Anon | 11:18:19 17/05/2013 |
НИНУЖНО | ||